Marco Teórico


Las ecuaciones cuadráticas se caracterizan por tener variables elevadas al cuadrado; también se llaman ecuaciones de segundo grado porque la expresión algebraica que las representa es un polinomio de segundo grado. Estudiaremos el caso más sencillo que es el de una ecuación cuadrática con una sola variable; estas ecuaciones se escriben de manera general como: 


ax² + bx + c = 0


Donde x es la variable de la ecuación y a, b y c son números reales. En este tipo de ecuaciones a no debe ser cero, ya que si esto sucede, a la ecuación se convertiría en lineal con una variable. Otra de las características de las ecuaciones de segundo grado es que tienen dos soluciones, que pueden ser número reales o imaginarios.
También pueden ser incompletas y completas. La solución de una ecuación cuadrática  ax²+ bx + c =0 a través de la fórmula general está dada por:

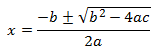
soluciones de la completa

En las fórmulas anteriores, la expresión b al cuadrado menos 4ac se conoce como el discriminante; se llama así porque determina si la ecuación tiene o no solución en los número reales. ƒ
·         Si b al cuadrado menos 4ac es positivo la ecuación tiene dos soluciones. 
·         Si b al cuadrado menos 4ac es negativo la ecuación no tiene solución real porque se tiene una raíz cuadrada de un número negativo cuya solución no existe en los números reales. 
·         Si b al cuadrado menos 4ac es cero entonces se tiene una solución doble.


Hecho por: Martínez Ortíz Valeria Guadalupe

Comentarios

Publicar un comentario

Entradas populares de este blog

Definición de función de segundo grado

Imagen
Función de segundo grado . La función es la relación de dos conjuntos, uno llamado dominio que contiene todos los valores posibles que pueden evaluarse en la función, y el rango, conjunto que tiene todos los valores resultantes de la evaluación de una función de forma que a cada elemento del dominio le corresponde un único elemento del rango. Las funciones de segundo grado o cuadratcas tienen las siguientes características: • La representación gráfica de esta en un plano sera una parábola. • La variable x se puede expresar como: f (x)= ax^2 + bx + c. • Generalmente se usan las letras: f, g, h   Minimamente: s, x, u, t, F, G, H. Ejemplos:  Hecho por: Rodríguez Cuautle Josué
Leer más

Aplicación de la función de segundo grado

Imagen
1ra. Aplicación: MATH 42 es una aplicación que puede servir al alumnado para entender mejor las matemáticas, lo puede ayudar en la realización de los ejercicios, tanto en el caso de los deberes, como en la preparación de los exámenes.  Primer paso Introducir el problema en la calculadora, después pulsa en mostrar mas opciones. Paso dos Elija una sugerencia y obtendrá una solución paso a paso de su problema. Tercer paso Pulse los triángulos azules, con el fin de comprender mejor los pasos de la solución. Cuarto paso Pulse una frase y obtenga una definición. Quinto paso Pulse el icono gráfico u obtenga un gráfico interactivo de su problema  2da. Aplicación: Editex matemáticas. Estas apps permitirán a los alumnos acercarse de una manera sencilla y amena a los contenidos y a la realización de actividades y ejercicios matemáticos.  Este programa cuenta con diferentes opciones, la primera es la de teoría donde puedes resolver tus dudas con ...
Leer más

Relación de función y ecuación de segundo grado.

RELACIÓN ENTRE FUNCIÓN Y ECUACÓN DE SEGUNDO GRADO Una   ecuación de segundo grado ​ o   ecuación cuadrática de una indeterminada   ​es una   ecuación   que tiene la forma de una suma algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un   polinomio   de   segundo grado   o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática de una variable es: ax^2 + bx + c = 0, donde a no es igual a 0 Donde   x   es la   variable , y   a ,   b   y   c   constantes;   a   es el   coeficiente   cuadrático (distinto de 0),   b   el coeficiente lineal y   c   es el término independiente. Este polinomio se puede interpretar mediante la   gráfica   de una   función cuadrática , es decir, por una   parábola . Esta representación gráfica es útil, porque las intersecciones o p...
Leer más